Trigonometric Identities Pythagorean Relations. A trigonometric identity is an equation that involves trigonometric functions and is true for every single value substituted for the variable (assuming both sides are defined for that value) you will find that using this first pythagorean identity, two additional pythagorean identities can be created. Pythagorean trigonometric identity is a trigonometric identity expressing the pythagorean theorem in terms of trigonometric functions.
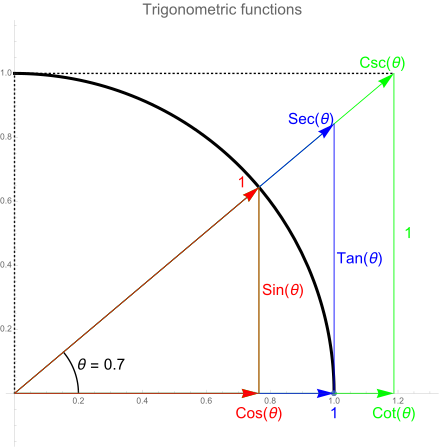
Ccss.math.content.hsf.tf.c.8 prove the pythagorean identity sin 2 (θ) + cos 2 (θ) = 1 and use it to find sin(θ), cos(θ), or tan(θ) given sin(θ), cos(θ), or tan(θ) and the quadrant of the angle.
The sum of the areas of the two squares on the legs (a and b) equals the area of in mathematics, the pythagorean theorem or pythagoras' theorem is a relation in euclidean geometry among the three sides of a right triangle. The pythagorean identities are examples of trigonometric identities : The pythagorean identities can be very useful for simplifying complicated trig statements and equations. These can be trivially true, like x = x or usefully true, such as the pythagorean theorem's a2 + b2 = c2 for right triangles.
Komentar
Posting Komentar